n-body gravity simulation

About

After implementing the Barnes-Hut algorithm for Ship Crew RPG, I realized that I could gain an even simpler, yet more aggressive optimization: stop simulating tiny objects’ gravitational mass.

This allowed me to simulate several thousands of stars in ROBLOX. That won’t sound very impressive to a C developer, but for Lua it’s pretty good!

Gifs

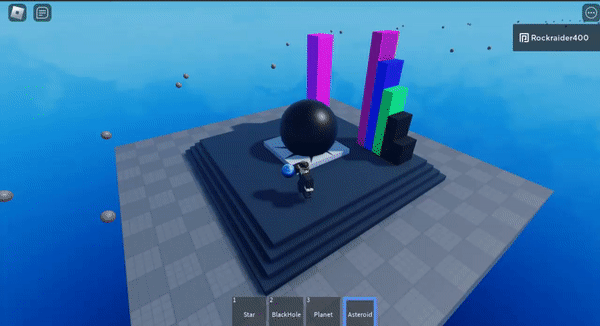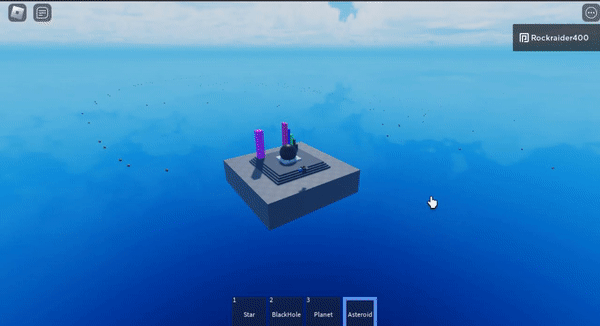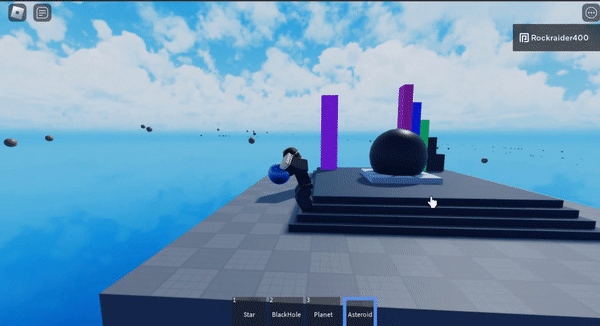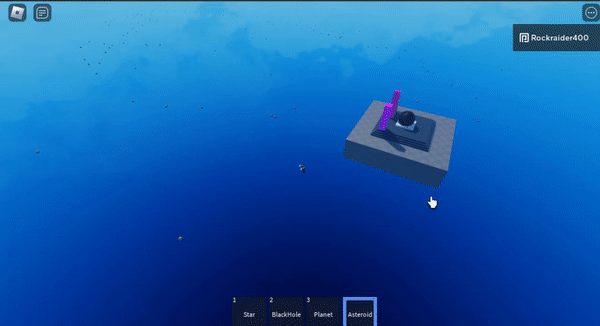
I <3 gravity

These are actually naive n-body simulations (every star has gravitaitonal mass) but they’re really cool so I wanted to include them

Optimizing n-body simulations with Barnes-Hut algorithm

You can play/edit this demo on ROBLOX here.

The premise of my Ship Crew RPG game is that the universe is at least one galaxy, built out of star systems, where planets orbit stars and moons orbit planets and so on. All of the gravity is actually simulated.

I want to have a big galaxy, which means a lot of physics computations – so I decided to research an optimized gravity algorithm called the Barnes-Hut algorithm.

Before I dive into that, I have a couple of quick side notes:

#1 Physics simulation is broken up into sub-environments

I want to be clear that in Ship Crew RPG, it’s not just one big physics environment. A really important design goal is that characters are able to walk around “inside” big, moving structures like ships and planets and moons.

To achieve that, the “interior” environments of ships and planets are actually kept separate and stationary, and I explicitly write code for transitioning between the environments. I made a tech demo for this here, and it’s also evident in the proof of concept for Ship Crew RPG.

#2 The biggest optimization is just doing less gravity.

Barnes-Hut is great – but I discovered an even more powerful optimization: don’t simulate the gravity of small objects.

For example, if you’re simulating a galaxy, then you don’t need to calculate how much the stars pull on the black hole/center of mass of the galaxy because it doesn’t matter.

If you only have a handful of massive objects, this effectively reduces time complexity from O(n^2) to O(n).

We can get away with this for Ship Crew RPG because of point #1 – a galaxy-level environment is literally only concerned with the gravity of stars (tiny) and black holes / galaxy mass centers (massive).

I have a demo of this here.

And now, for Barnes-Hut

With all that being said, it was really fun to implement the Barnes-Hut algorithm and the experience was definitely worth it. Let me show you what I made.

If you want to understand how the algorithm works, I highly recommend these two sources.

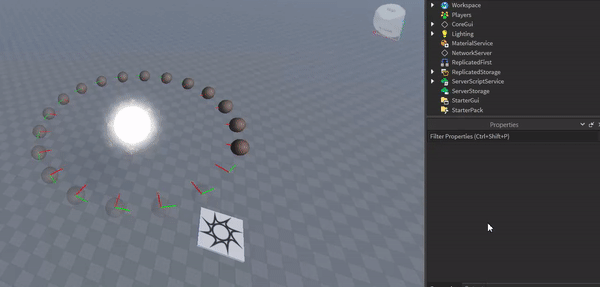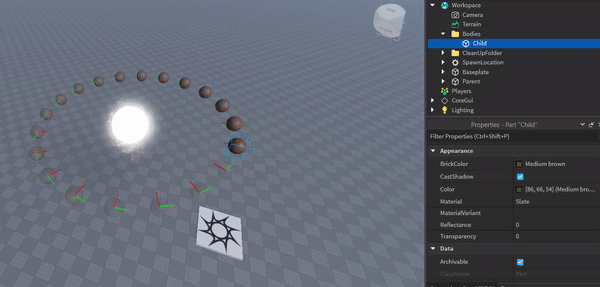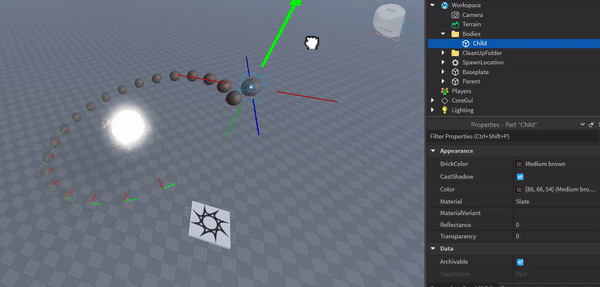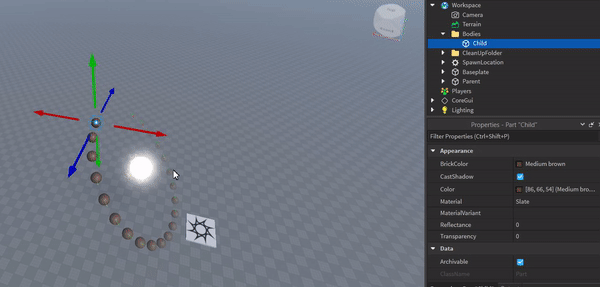
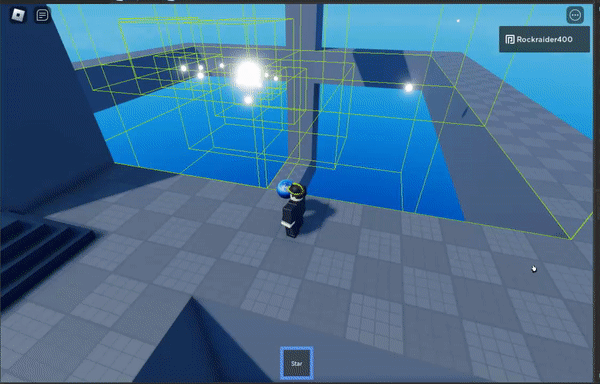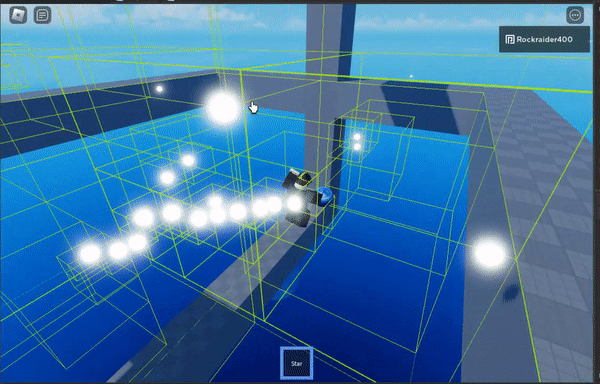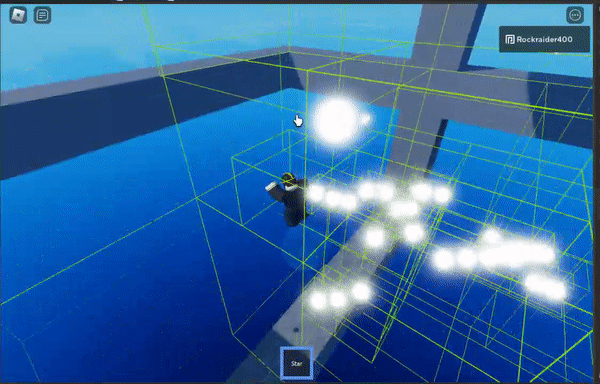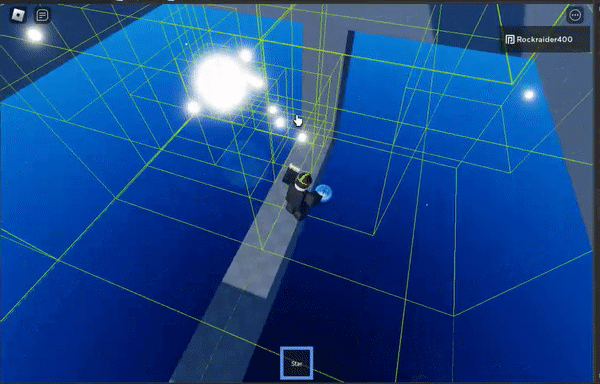
The gist of the algorithm is that clusters of bodies can be approximated as a single point when you’re far enough away from the group. For example, this moving system could be approximated as a single body:

You can play/edit this demo on ROBLOX here.

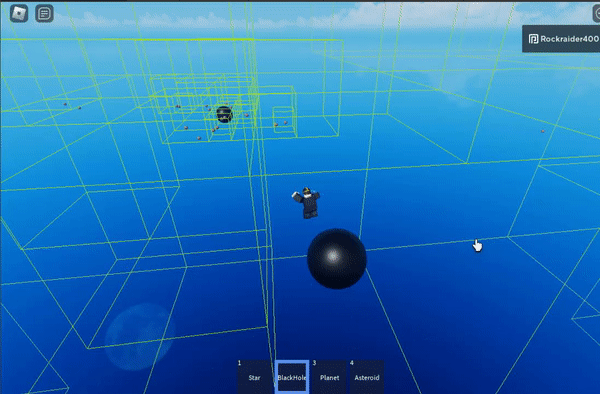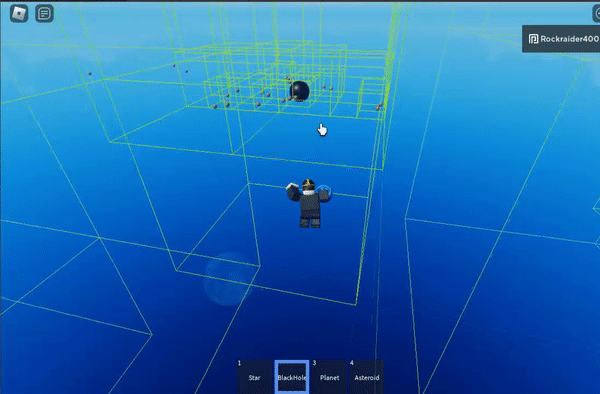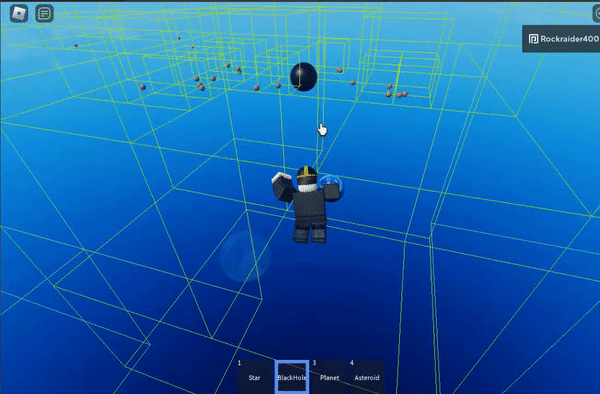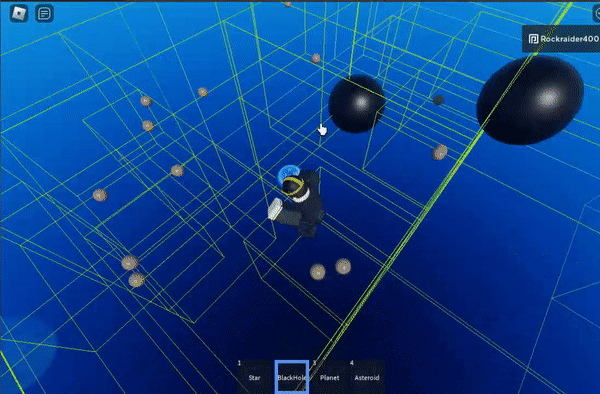
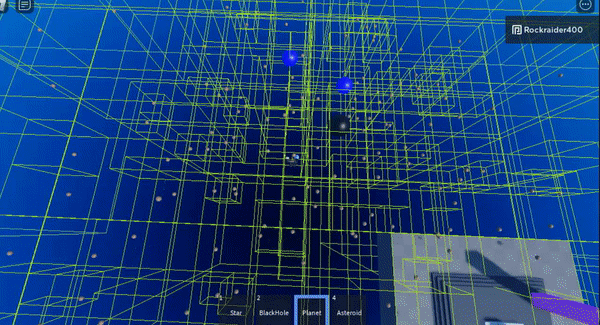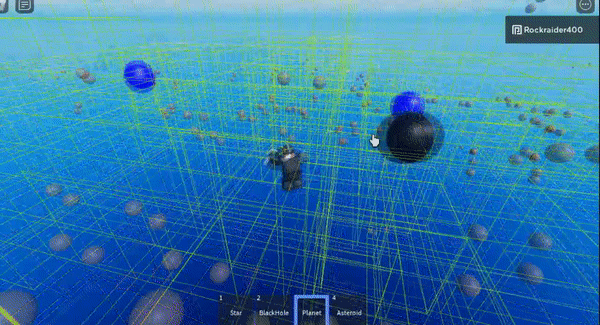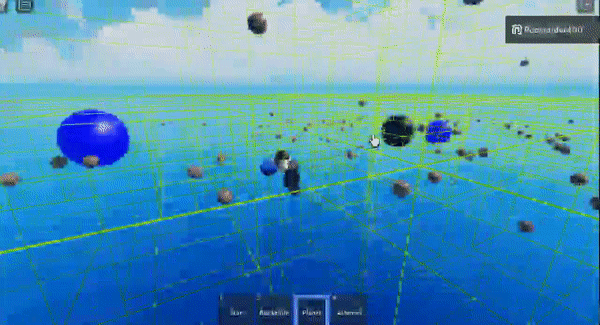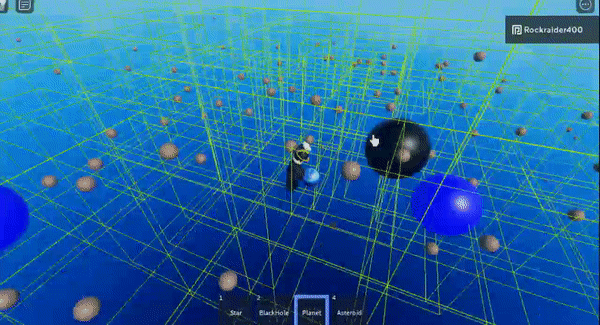
The green boxes are the cells of the octree, the spatial partioning structure that makes this work

Of course, if you’re too close to the cluster of objects like in this gif, then you would just calculate gravity between every pair of objects normally.

(there are no collision implemented in this demo)

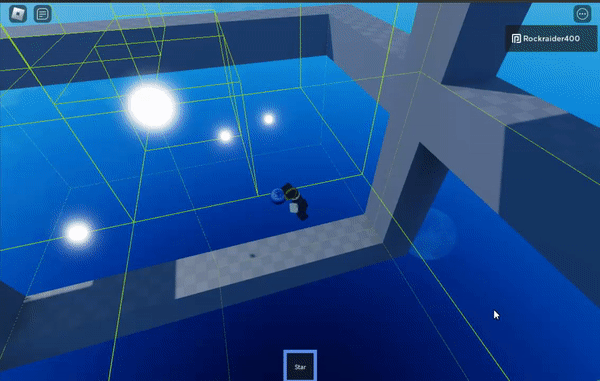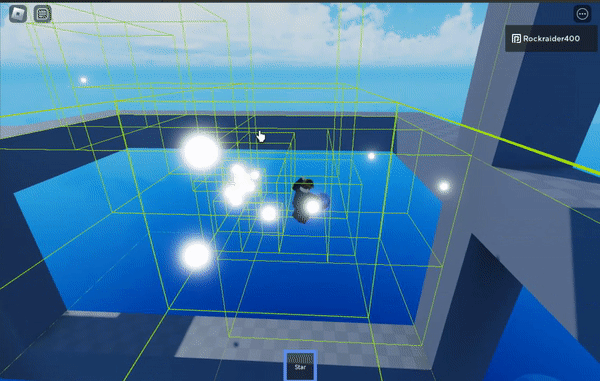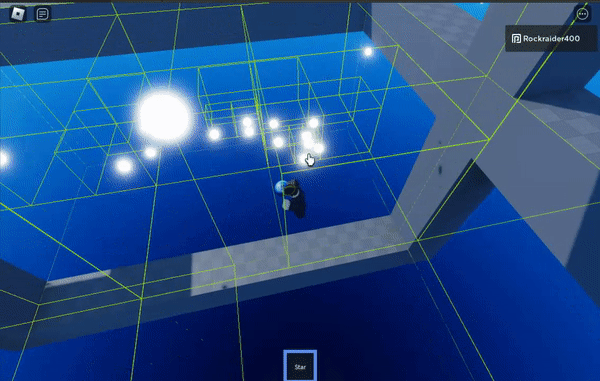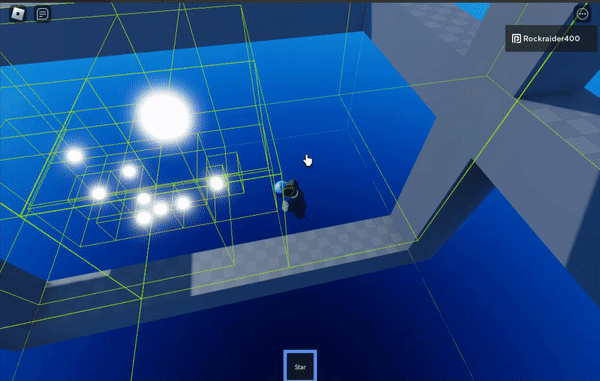
Octrees are finite in size – the grey parts outline the edge of the octree.

I don’t have a gif showing it, but the stair-stepped, colored blocks change the distance at which the algorithm switches from high-precision calculations to approximating large swathes of points. The shorter the distance you start approximating at, the more efficient the algorithm is– but the less precise it becomes.

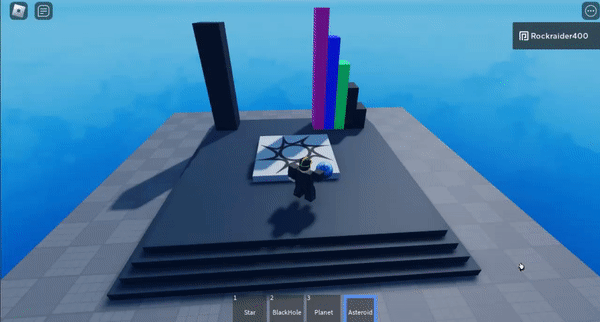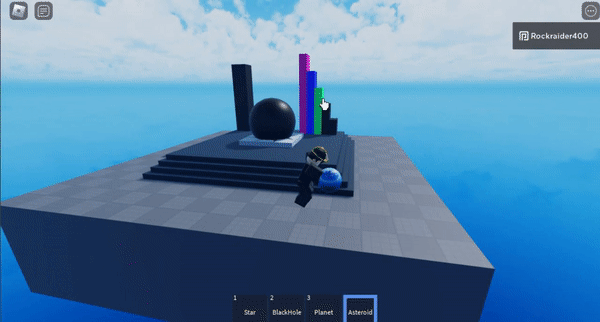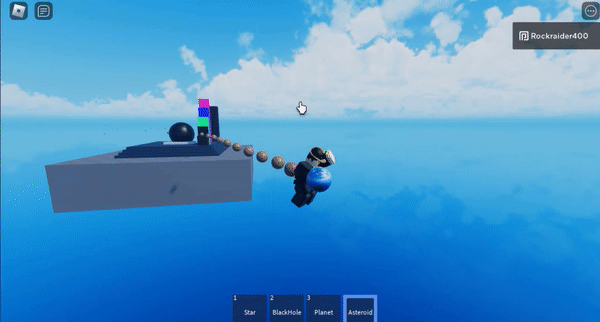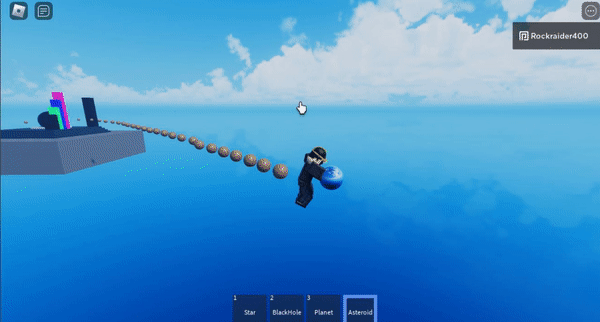
The purple block sets approximation at the highest distance threshold, which is least efficient but most precise.

Barnes-Hut works well because, when simulating gravity between galaxies, it is very common for spread-out clusters of stars to exist, which is the condition Barnes-Hut exploits.

There’s a “sweet spot” distance from a gravitational center where bodies can orbit in a circular path

Great success

More gifs

I’m not gonna lie, it was really fun to play around with this tech demo.

I think I hit the rendering limit lol

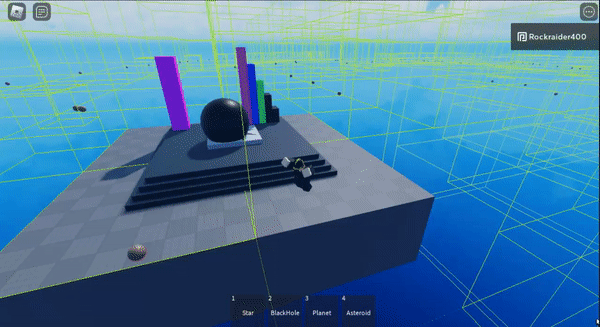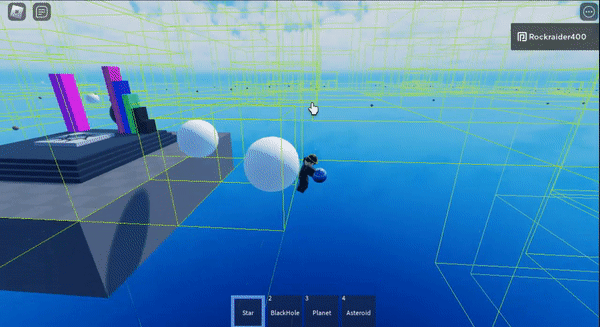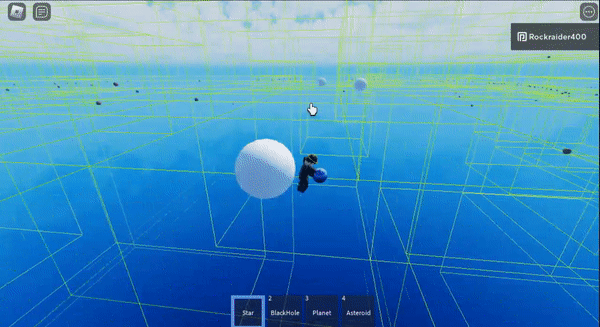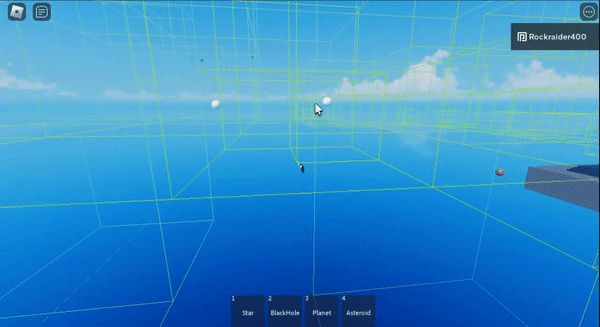
If you throw stars at a black hole you can fling it into outer space

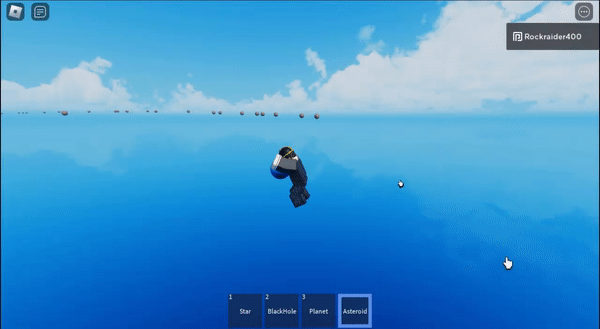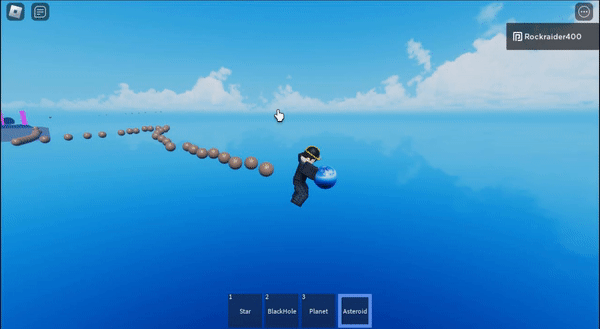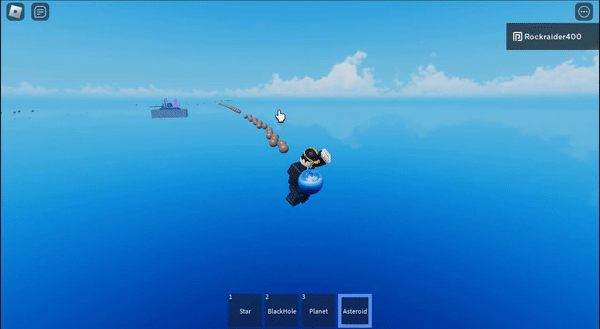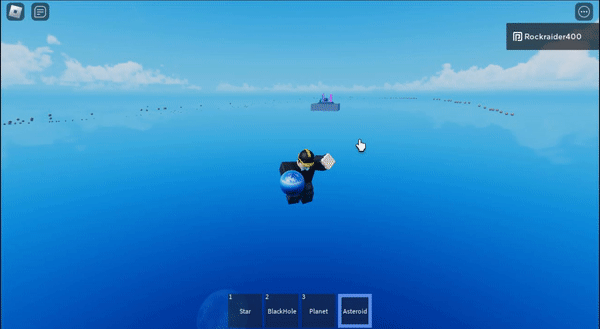
I made an asteroid machine gun and then sucked them all into a star

And then if you shoot the asteroids at the star, they get flung really far

10/10 tech demo. Would build again.

Quadtrees

While researching the optimized n-body gravity simulations for my Ship Crew RPG game, I had to implement a quadtree / octree data structure so that I could implement the Barnes Hut algorithm.

A quadtree (2 dimensional) or octree (3 dimensional) is a spatial partioning data structure that allows you to quickly retrieve a set of points that are in a given region of space.

In the context of the Barnes-Hut algorithm, a quadtree or octree allows us to easily approximate a set of far-away points as just one gravitational mass, which reduces time complexity from O(n^2) to O(n log n).

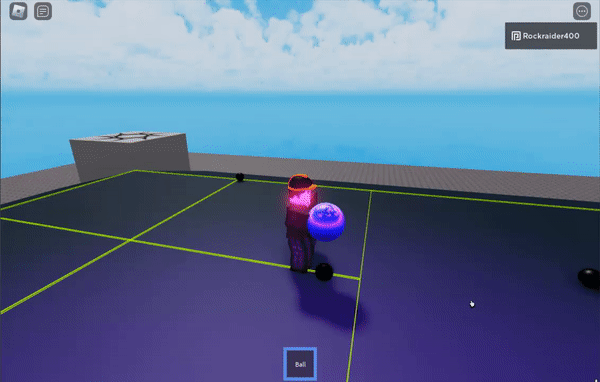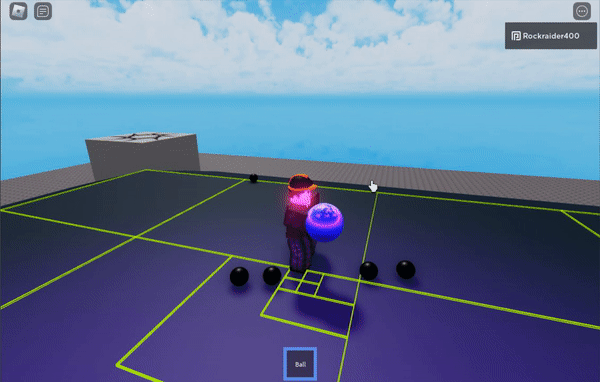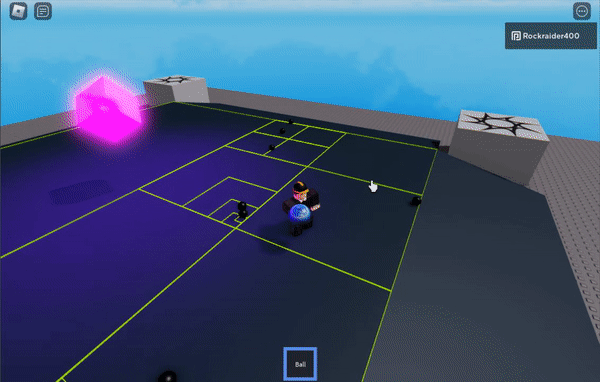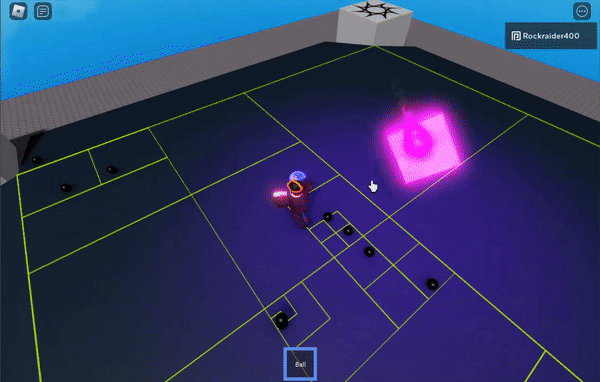
Here’s a demo ROBLOX place

You can play/edit this demo on ROBLOX here.

Each ball gets its own cell, generally speaking. Smaller cells are children of bigger cells.

The purple crystal erases the board

Cell size has a minimum limit to avoid infinite recursion (and stack overflow) when coincident points are introduced.

Unpolished quadtrees

This is an earlier version of the quadtree:

(The points are randomly added)

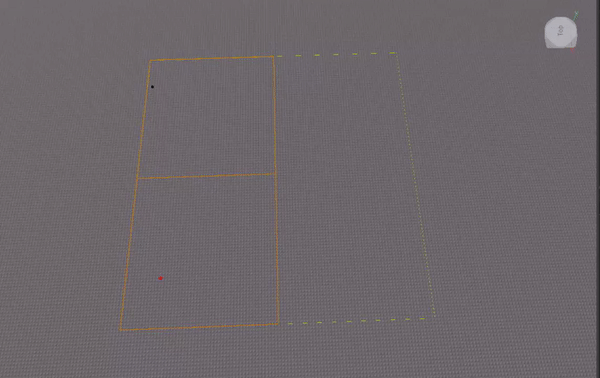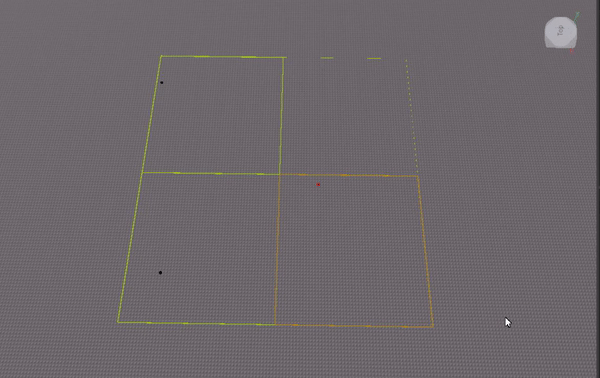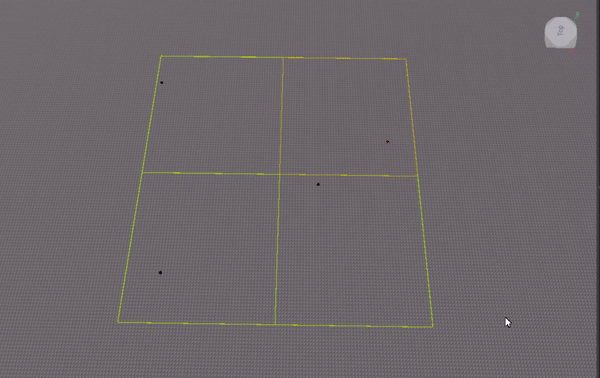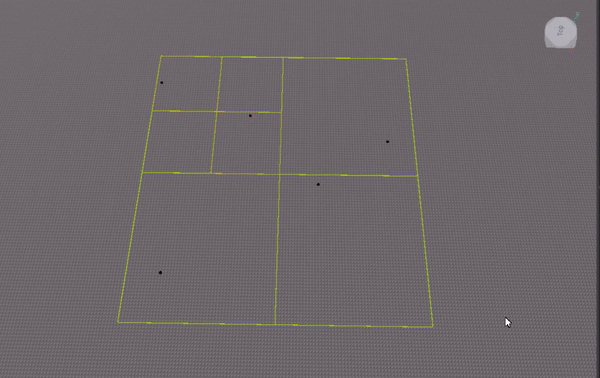
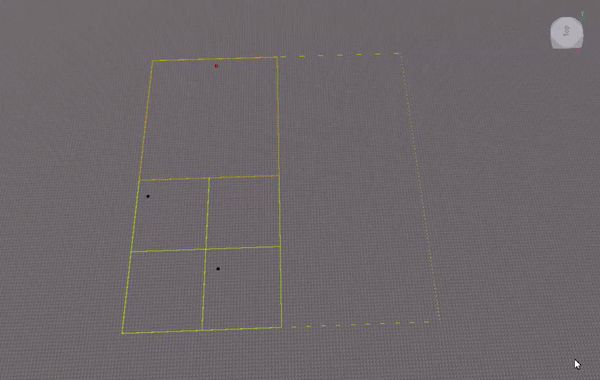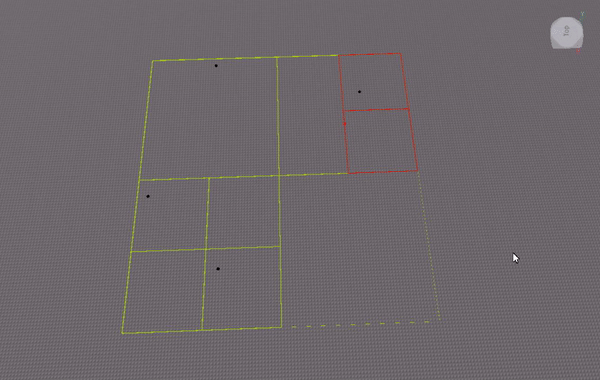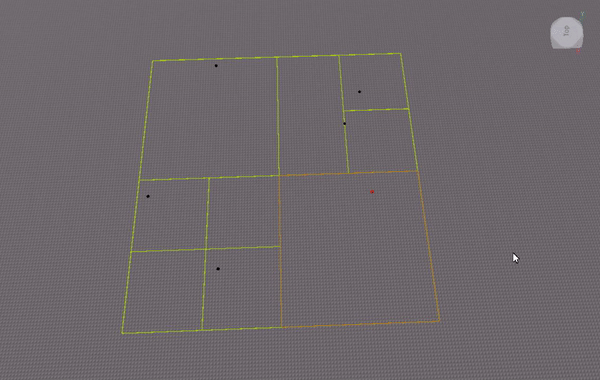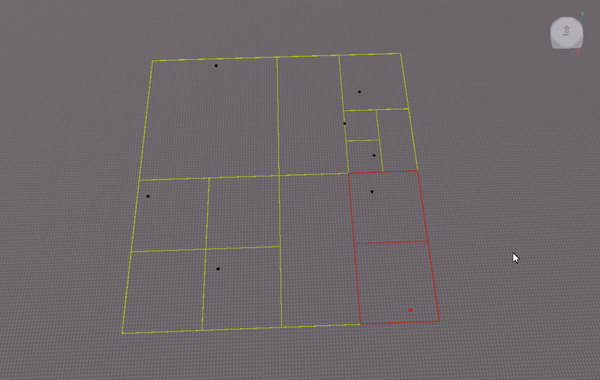
I experimented with implementing the quadtree as an array (similar to how one can implement a binary tree as an array). This gif visualizes where nodes are stored in the array:

And these are 3D Octrees, so-called because they have eight octants instead of four quadrants.

Slow

Speedy

Orbital path predictor

While playing with n-body gravity simulations, I found it difficult to construct stable orbits – so I prototyped a quick orbit calculator. It works by simply running 100 or so iterations into the future to predict the orbital path. It doesn’t account for the movement of the large gravitational mass. The mathematics can also be applied to construct stable orbits automatically.

Gifs