2D Polar Collisions

Motivation

This is part of my research into developing my own physics engine for Ship Crew RPG. Part of the game entails walking on round planets, so I developed collisions for a character’s hitbox and a tilemap arranged in polar coordinates so I could make a Terraria-style grid of blocks for round worlds.

This was a lot harder than I thought it would be!

Implementing 2D collisions for AABBs (Axis-aligned bounding boxes) is relatively straightforward for normal, flat, Cartesian coordinates. It is not so easy for polar coordinates.

You can play/edit this demo on ROBLOX here.

One of my early attempts. Notice how the character slips into the blocks

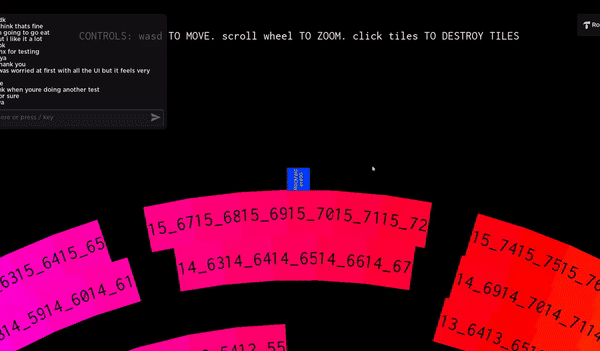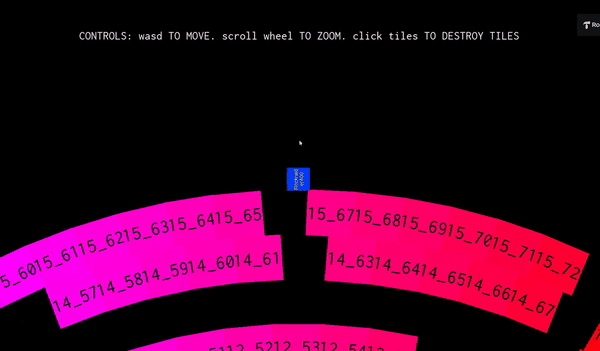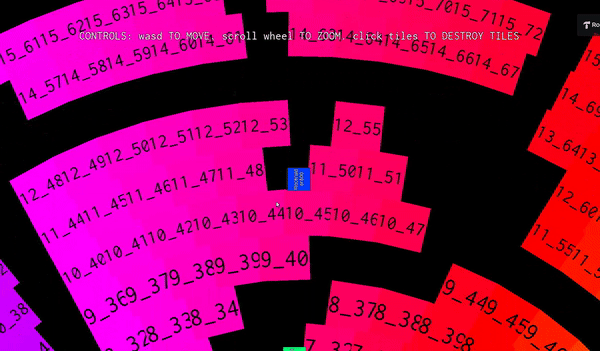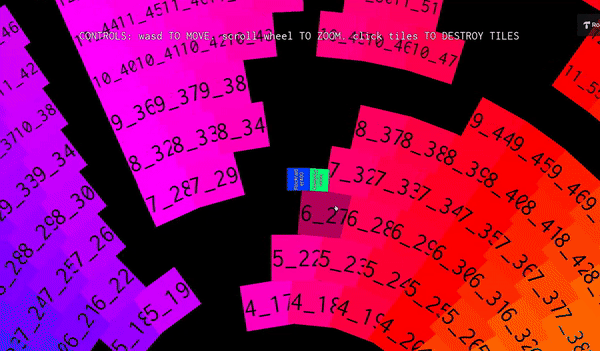
I was so relieved when I finally got it work

What are polar coordinates?

Coordinate systems are used to measure any point in space. We’re working in 2D (2 dimensions) here, which means that we use two numbers to describe where something is in space – like on a sheet of paper.

In Cartesian coordinates, you take two rulers and turn them 90 degrees to one another. For any point in space, you can measure its distance along the first ruler (call that number X) and the second ruler (call that number Y), and you have a unique “address” for that point. You can do this for any point in space.

That’s not the only way to measure space. Polar coordinates are like measuring points based on where they are on a bull’s eye. Your first number (call it R) will be how far the point is from the center, or in other words – how many rings away from the center it is. The second number (call it θ – the greek letter “theta”) is the angle the point is at – kind of like the different hours on an analog clock.

I picked polar coordinates because they allowed me to define a grid of blocks for a round planet mathematically equivalent to a normal grid of blocks, like in Terraria or Starbound. At least, it was almost mathematically equivalent.

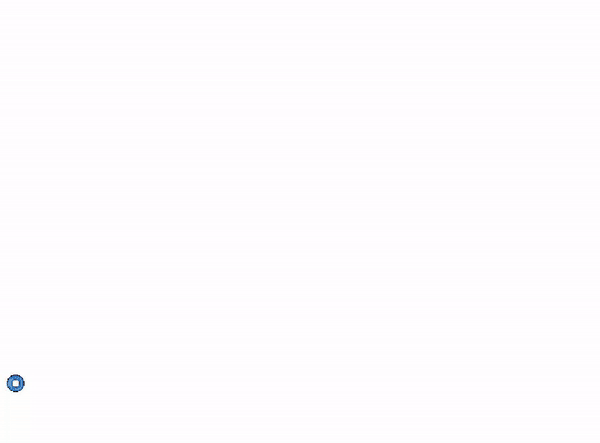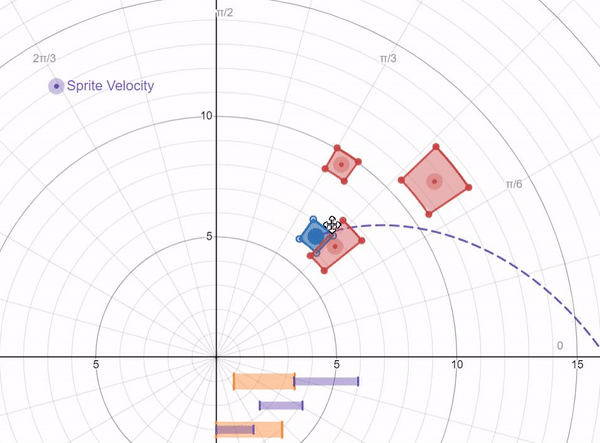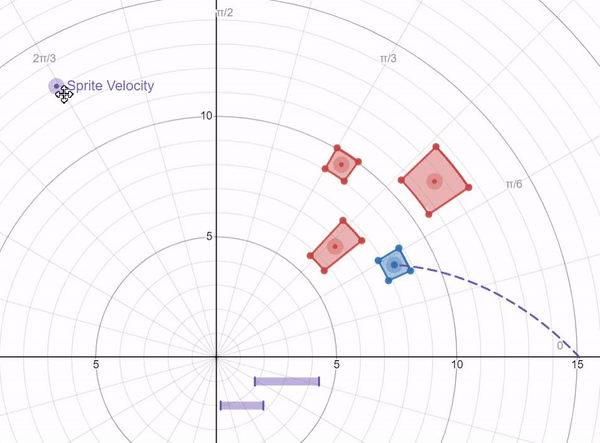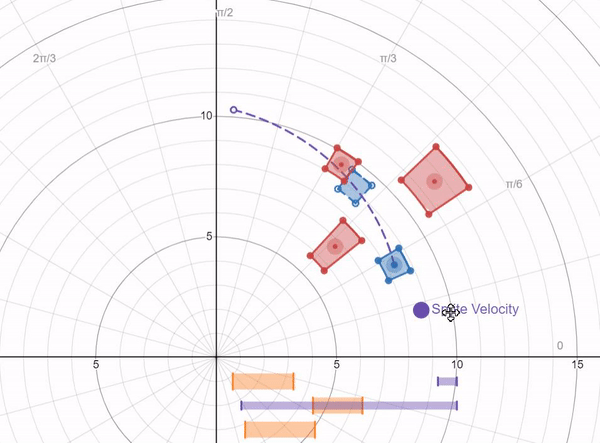
A collision math model I developed using desmos.com. Notice the concentric rings (measuring R) and angular values measuring θ: π/6 (30 degrees), π/3 (60 degrees), π/2 (90 degrees), etc

Polar coordinates are not as easy as I thought

Polar collisions are different from Cartesian collisions in three important ways:

1. The central pole has weird behavior if you fall through it
2. The character doesn’t collide with blocks when crossing from θ=0 degrees to θ=359 degrees, or vice versa
3. You have to resize the character’s hitbox as their R position changes (and this broke my collision algorithm)

#1 Falling through the center of the world breaks collisions

Gravity is defined such that your character falls along the R dimension toward the central pole of the world. However, if you make it that far and keep falling, your character will then have negative values for R. It will still render, but won’t collide with anything because all of the blocks are defined solely for positive R values. When your character has a negative R coordinate, it is in the same position as if it had the same positive R coordinate and was rotated 180 degrees around the world.

The solution is simple – just don’t let characters’ R values go below a threshold:

Notice how there’s an “invisible” ground around the center. This is a “threshold” of R that characters aren’t allowed to go past.

Shoutout to AxisAngle, who is playing the tech demo with me here. He is a main developer on the ROBLOX game Phantom Forces by StyLis studios

#2 Collisions break at the (θ=0 degrees) boundary

Let’s say our world is a clock. When I travel around the clock, it’s normally continuous. This means that if I’m at 6, I either go to 7 or to 5 (if I’m going backwards). The difference between either of those positions is just one – there’s no big “jump”.

However, if I’m at 12, and I keep going clockwise / to the right – I get back to 1. There is a jump.

What that means for collisions is that, by default, the character won’t register collisions on the other side of that boundary. It’s mathematically equivalent to this scenario:

I just fall off the side of the world!

We have to do two things to solve this:

1. We have to make the θ position of our actually wrap around. We can’t allow for θ values greater than 360 degrees or less than 0.
2. When we’re overlapping the boundary, we have to simulate a second copy of the character but on the other side of the boundary, so we can register collisions with that side.

Like this:

Notice the temporary, yellow duplicate of the character – this allows us to be on both sides of the boundary at once.

In polar coordinates, it looks like this:

Wait, what’s wrong??

At this point in development, I thought I had understood all of the challenges in making polar collisions. But there was a big one I was still missing…

#3 You have to resize the character’s hitbox every frame (and this breaks collision resolution)

A slice of pie is wider at the back than at the front, but it subtends the same angle throughout the whole slice. Similarly, in polar coordinates, a block with the same angle gets wider as it travels away from the center of the world.

If we want our character’s hitbox to stay the same actual size, we have to change its angular size as we change altitude.

The formula for doing this is not complicated. The reason this is an issue is that 2d AABB collision algorithms – which are meant to be simple – are not usually designed for hitboxes that change size every frame.

What happens is that, as you fall, the angular size of your character gets bigger. If you are directly adjacent to a tile, then as you fall your character will expand into that tile and register a collision.

When collisions happen, normally my algorithm looks at the velocity of the character to decide whether to offset in the R direction or the θ direction – so if you’re walking laterally (θ direction) into a block, your velocity will be in the θ direction, and the collision resolution will push your character out of any block you walk into along the θ direction.

That works for most cases… except the case of falling while you get wider (in θ coordinates). While you’re falling, your velocity is in the R direction going down, but you’re actually colliding laterally in the θ direction. So the algorithm as defined so far will think that you need to be offset up instead of to the side. Let me show you what I mean:

The character slips into the floor here because the algorithm is resolving the collision in the wrong direction.

(You can also see how there’s a jittery feedback loop when I try to slide down the side of another block.)

Here you can see the character bounces off of block corners really weird. This is the same effect.

So ironically I was able to solve this edge case by using a worse collision resolution formula that I developed earlier on. It resolves the collision by looking at which dimension (R or θ) that the character is overlapping the block in more.

Ahh….

In ROBLOX Studio, I was still able to find an edge case where, when you jump on top of a block onto its corner, it still throws you under the ground. I was never able to replicate this in-game for some reason, so I consider this to be 99.9% complete.